2528時間目 ~BASIC~次の漢字の読みを記せ。レベルⅠⅠ 責善Ⅱ 聴請Ⅲ 玉照Ⅳ 人の子たるの礼、恒に言に老いを称せずレベルⅡⅠ 杞憂Ⅱ 奄虞Ⅲ 遅暮の嘆レベルⅢⅠ 屹屼Ⅱ 叕やかⅢ 啞子の夢特別問題A~数学~3sinθ+cosθ=3が成り立っているとき、sin2θの値を求めよ。Porinここはを読んだ際のメモや、感想などをまとめてるページなり! 目次 1 この本について (該当箇所へ) ︎ 読書メモゲームアプリの数学#5c1a167a1a4b8a0000de81ec 2 読書メモ START! (該当箇所へ) ︎ 読書メモゲームアプリの数学#5c1a167a1a4b8a0000de03 1 θ の定義式から求められます。 2つ目は sin 2 θ cos 2 θ = 1 。 これは、 三平方の定理 から求められます。 三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵 直角三角形において、「直角」をはさむ2つの辺の長さを a, b 、斜辺の長さを c としたとき \ (a^2b^2 3つ目は tan 2
三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典
Sin(π/2-θ)=cosθ 単位円
Sin(π/2-θ)=cosθ 単位円-θというのは、単位円を逆回りにθだけ回せばよいので、 x座標は変わらずcos\(\theta\)、y座標の正負が逆になりsin\(\theta\)になります。 \(\displaystyle tan \theta=\frac{sin \theta}{cos \theta}\)なので、 \(\displaystyle tan (\theta)=\frac{sin (\theta)}{cos (\theta)}\) 数学4-2 2) 負角、余角、補角の式変換 三角比を含む計算問題の中には、sinθやcosθの「θ」の部分が複雑なものになっているときがあります。 具体的には、sin (-θ)やcos (π/2-θ)、sin (π-θ)といったようなものが挙げられます(ほかにも色々あります




正割余割 三角関數 Retdy
tan(π/2-θ)=sin(π/2-θ)/cos(π/2-θ)=cosθ/sinθ=1/tanθとなります 」 ⑧「同様にして(ⅵ)のπ/2θの方の公式も単位円で確認してみます。 π/2θの位置は、π/2進んで、そのあとさらにθ進んだ位置となり、θのときの直角三角形と合同な直角三角形ができます。1999年 東京大学・理文共通 数学 第1問 おはようございます,ますいしいです 本日第2弾目のアップです ともかく寒い これらを使って、 cos (θπ/2) = cos ( (θπ/2)π) = cos (θπ/2) = cos (π/2θ) = sinθ sin (θπ/2) = sin ( (θπ/2)π) = sin (θπ/2) = sin (π/2θ) = cosθ この2式を使って、θ = φπ/2 と置けば、 cosφ = sin (φπ/2) sinφ = cos (φπ/2) それとも、sin, cos をべき級数で定義して、 4式の成立を計算で示して欲しいのか? 2
ねとらぼ nlabitmediacojp「テストで電卓使ってもいいよ!」 日本と米国の数学、考え方の違いとは? 期末考査が終わって少し時間が取れたので、彼が丸暗記したという三角関数の公式の成り立ちを単位円を使って説明しました。 sin(θ2nπ)=sinθ cos(θ2nπ)=cosθ tan(θ2nπ)=tanθ sin(θ)=sinθ cos(θ)=cosθ tan(θ)=tanθ sin(θπ)=sinθ cos(θπ)=cosθ tan(θπ)=tanθ sin(θπ)=sinθ sin(θπ)=cosθ tann(θπ)=tanθ sin(θπ/2)=cosθ cos(θπ/2)=sinθ tan(θπ/2)=1/tanθ sin(π/2-θ)=cosθ cos(π/2-θ)=sinθ tan(π/2-θ)=1/tanθ は、そういう意味です。 90°は、ラジアンにすると、π/2=9/18π。 cos 5/18π=sin 4/18π=sin 2/9π よって、 -cos 5/18π =-sin 2/9π 次は、sin 7/9π 。 これも第2象限に動径があります。 sin 7/9π=sin 2/9π です。
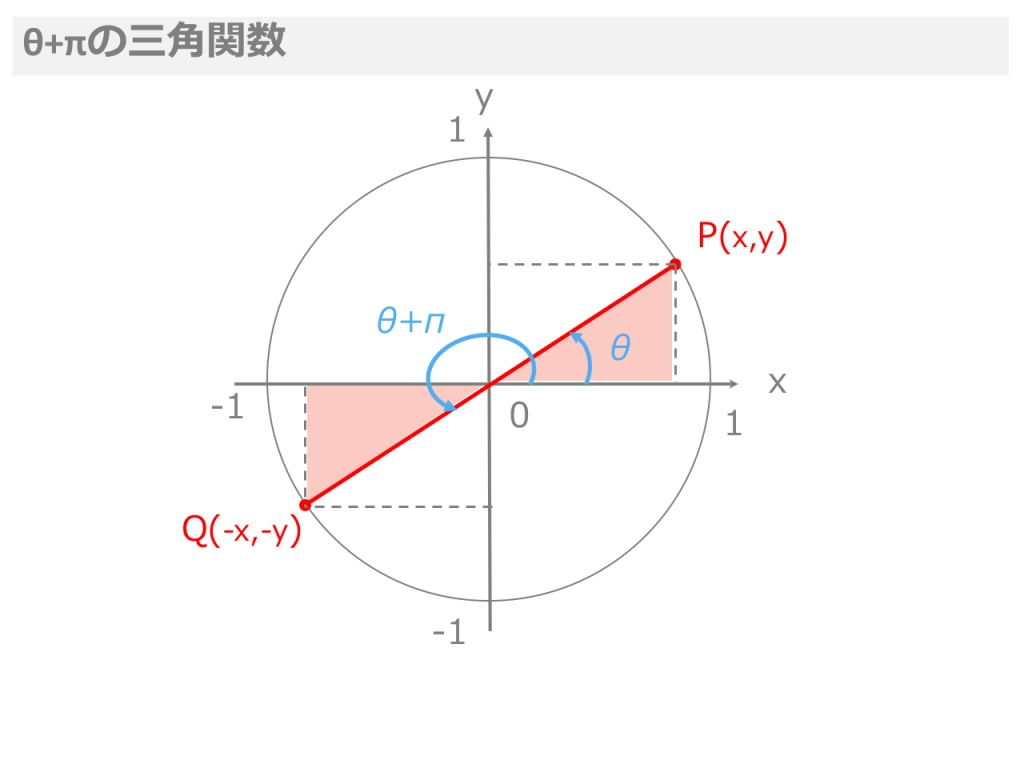
この事から、 sin(π/2 – θ) = cosθ cos(π/2 – θ) = sinθ である事も明らかであろう。, 周期関数において、その数値の振れ幅を『周期』と言うが、三角関数のsin、cosは、周期2πの周期関数という事にな加法定理の応用 テスト勉強中に分からない問題がでてきて困っています; 加法定理の応用(2倍角、半角)の問題で 「π/2<θ<π , sinθ=2/3のとき sin2θ , cos2θ , tanθ/2の値を求めよ」 というものなので0 6 S 4 S 3 S 2 S S 2 3 S 3 4 5 6 S S sinT 0 1 2 2 2 3 2 1 3 2 2 2 1 2 0 cosT 1 3 2 2 2 1 2 0 1 2 2 2 3 2 1 tanT 0 1 3 1 3 3 1 1 3 0 S 7 6 S 5 4 S 4 3 S 3 2 S 5 3 S 7



三角方程式の問題の解き方4タイプをイラスト付きで分かりやすく解説



Hugepdf Com Download No8a Pdf
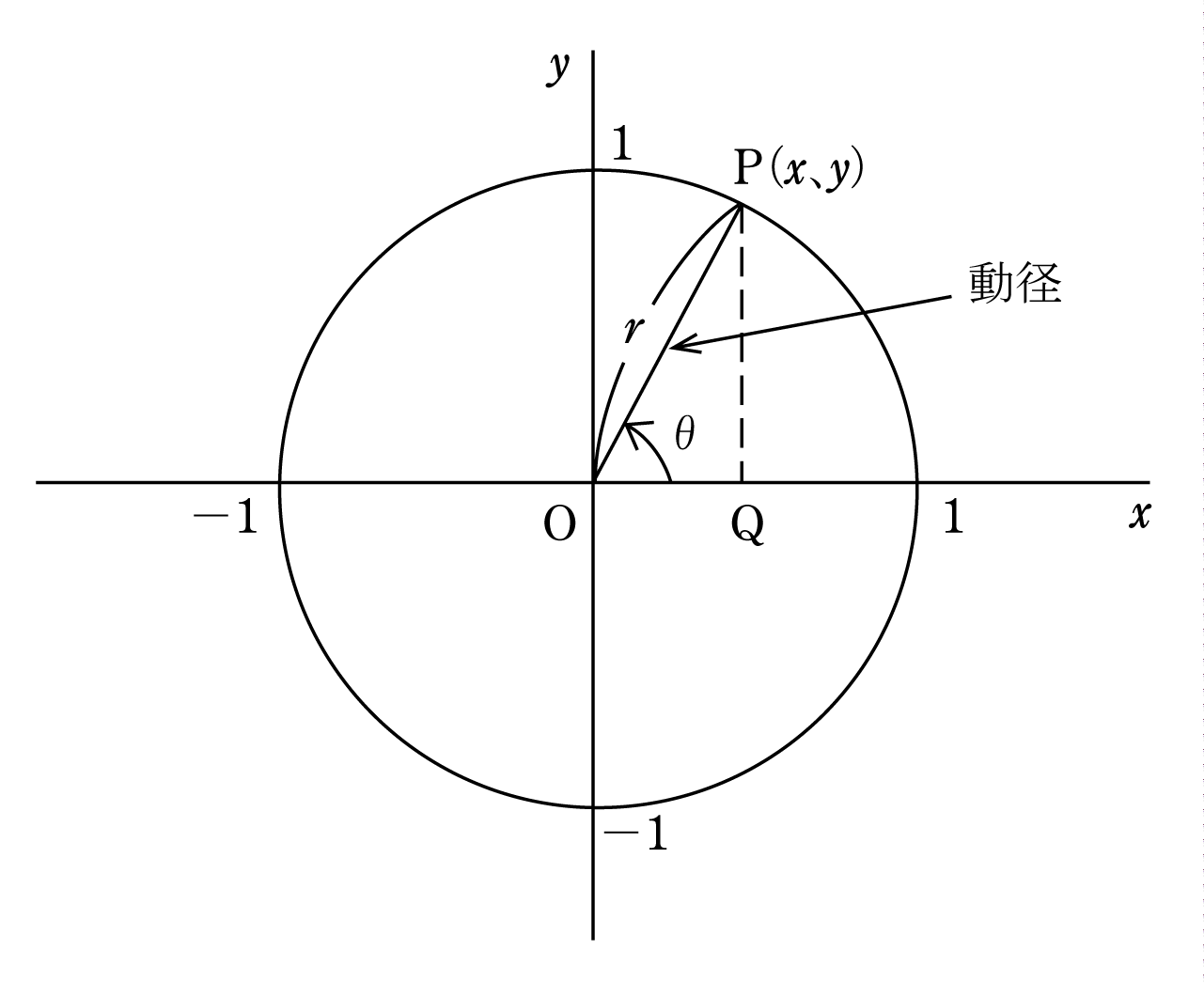
和角公式及解三角形答案我已经知道了 已知sinα=2/3 ,α是第二象限角,cosβ= (3/4)>即负四分之三, 1年前 3个回答 図で解る(単位円) 左の図 sinθ=青/赤、cos(θπ/2)=緑/赤 青=緑 ∴sinθ=cos(θπ/2) 右の図 cosθ=緑/赤、sin(θπ/2)=緑/赤 緑=青 ∴cosθ=sin(θπ/2)Math0101「角度を座標にする三角関数sinとcos」でご説明したとおり、角度θに対する単位円上の点(x, y)を定めたのが、三角関数sinとcosです。つまり、x = cosθ、y = sinθは単位円の円周を表します。




高校 数学 三角関数11 8 P 2 17分 Youtube




単位円上の点pと三角関数の結果をprocessingで描画する Jakaladaのブログ
僕なりの考え方は sin(π/2θ)=ーsin(θπ/2) に変形して単位円を使い座標が (x,y)から(y,x)に変わるから sin(π/2θ) =ーsin(θπ/2) =ー(ーcosθ) =cosθ という風に考えていて、これでは複雑で大変なので、もっと簡単で単純な解き方はないかなと思って質問しました。ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる: sin θ = ± 1 − cos 2 θ {\displaystyle \sin \theta =\pm {\sqrt {1\cos ^{2}\theta }}}Sin(π2θ)=cosθ 単位円 関連ニュース 「テストで電卓使ってもいいよ!」 日本と米国の数学、考え方の違いとは?




数学の質問です お願いします 456 In P 2 0 Sinnxd Okwave



3分で分かる 三角関数の基礎知識 合格サプリ
(3) 単位円の周の半分=πが √1(y') 2 の1,1での定積分値であること 2) ) (4) 円周の弧の長さが外側を通る折れ線より短いこと (5) lim x→0 sin(x)/x = 1 であること 高校数学では(1)を前提として話を進めているように見えます。I like mathematics and I am a C# programmer I also got overwatch banned on CSGO cause I'm a mad hacker I play CSS now tan (1) < π/2 円周率が305以上であることを示せ。 単位円に内接する正8角形の半周の長さを求める。 x=y>0, xxyy=1 より (x,y)= (1/√2, 1/√2) となる。 正解っすね。 他の解き方としては三角関数を用いたり、ルート2の近似値を直接用いて解く方法もあったり



T 1 Sine Cos 2 Sin Descubre Como Resolverlo En Qanda
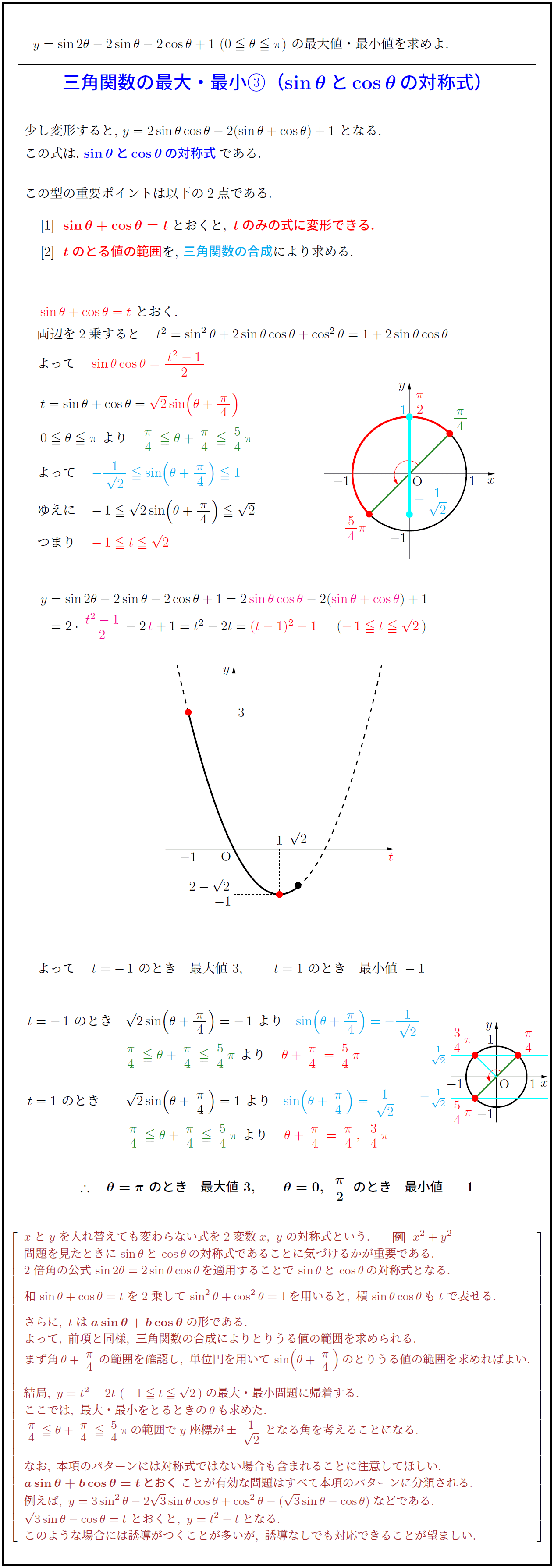



高校数学 三角関数の最大 最小 Sin8とcos8の対称式 受験の月
Sin(π2θ)=cosθ 関連ニュース 三角関数を思い出してみる どこでもサイエンス(147) マイナビニュース newsmynavijp三角関数を思い出してみる どこでもサイエンス(147) マイナビニュース 「テストで電卓使ってもいいよ!」 数学・算数 数学「三角関数」の問題が分りません。教えてください 0≦θ≦πのとき、次の方程式、不等式を解いてください。(途中式もお願いします。) (1)sinθ√3cosθ=2 (2)sinθ- 質問NoSin(π/2θ)=cosθ cos(π/2θ)=sinθ を得る。 これらの式は、単位円を使って左辺の値はsinθ、sinθ、cosθ、cosθのいずれに等しいかを考えれば求めることができる。 また、tanについては、tan=sin/cosから求めることができる。 加法定理 sin(αβ)=sinαcosβcosαsinβ cos(αβ)=cosαcosβsinαsinβ また、tan(αβ)=sin(αβ)/cos(αβ)より、



Kaminodrill Sakura Ne Jp Counter Php Pid 373




単位円を使いこなそう2 三角方程式基礎編 Sin 8 1 2 Cos 8 1 2 Youtube
sin(θπ/2)=cosθ cos(θπ/2)=sinθ tan(θπ/2)=1/tanθ sin( π/ 2θ)=cosθ cos( π/ 2θ)=sinθ tann( π/ 2θ)=1/tanθ の部分(網掛けになっている)が、彼は丁寧にマーカーで塗っているので、目に飛び込みました。 三角比とは? 三角比とは、長さの測量のために生み出された概念で、直角三角形の \(\bf{2}\) 辺の比を角度を使って表したものです。 直角三角形の場合、\(1\) つの鋭角の大きさを決めるとすべての角の大きさが決まり、辺の比も決まります。残り 2 つの交点が (cos(π/2θ), sin(π/2θ)) と (cos(3π/2θ), sin(3π/2θ)) になる という驚きの性質、これが起こるなんて本当に驚きです。 これを、らすかるさんのコメント (接点ではない)交点のx座標は±2t√(1t^2)となりますので から思い付けたのでしょうか?




16 合成公式はsinだけじゃないんです 医学生gの数学ノート




三角関数の単位円の問題が分かりません 風邪で学校を休んでいたら全く分から Okwave
cos(θπ/2)=cosθcosπ/2sinθsinπ/2 になります ここで単位円を書いてわかるように、cosπ/2=0、sinπ/2=1なので答えはsinθになります よく使う公式だったと思うので覚えといた方がい 3年弱前 ソ フ ィ ア cos (π/2θ)はなぜSinθなのですか? ?Textbook solution for Glencoe Algebra 2 Student Edition C14 1st Edition McGrawHill Glencoe Chapter 131 Problem 41PPS We have stepbystep solutions for



Http Www Eng Kagawa U Ac Jp Miyagawa Misc Math Basic Formula Miyagawa Pdf




先程答えてくださった人には申し訳ないですが理解できなかったので質問させていただきます Clear
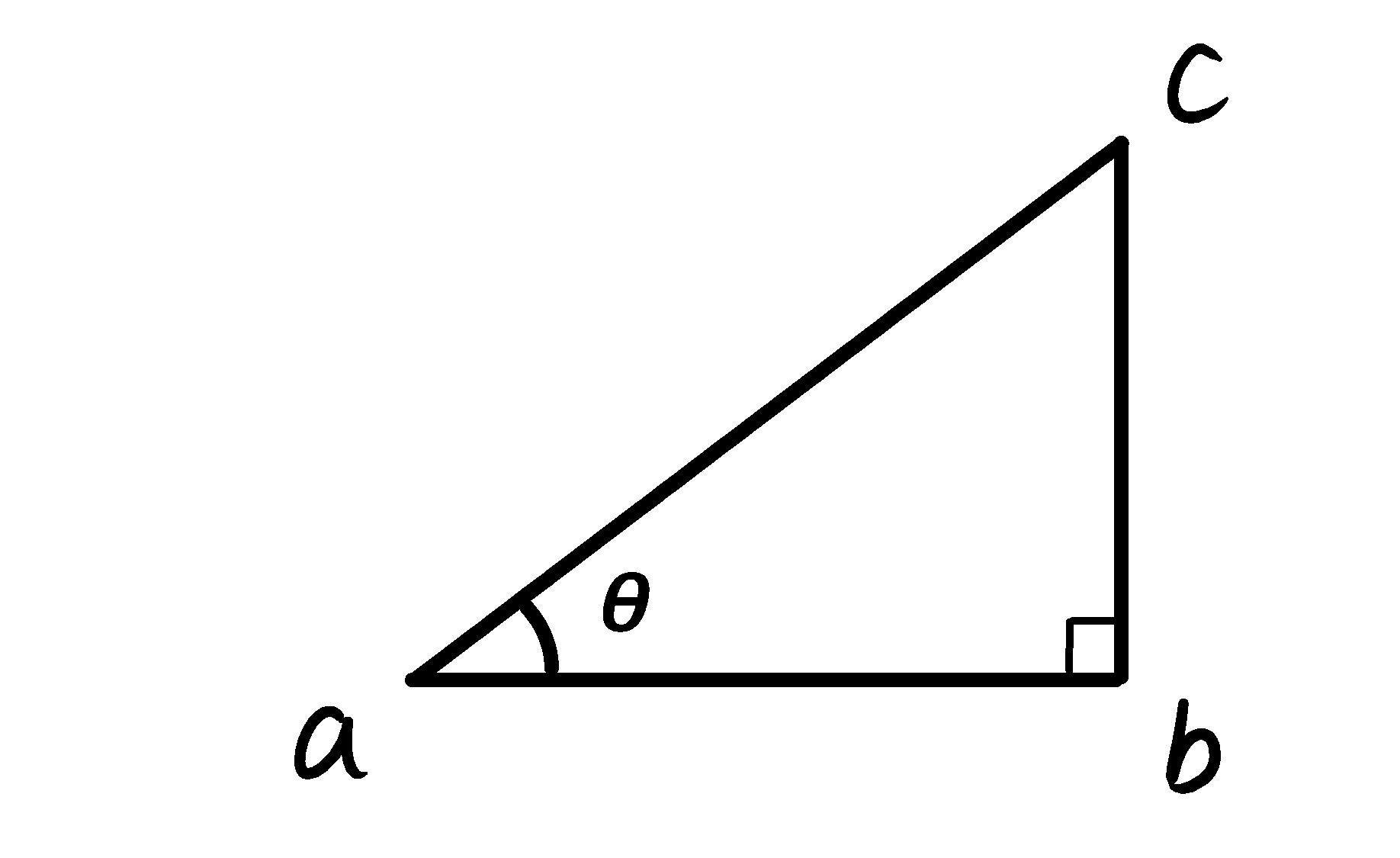
方の定理において、a =sin θ、b =cos θ、c =1 とすればよい。 1 sinθ θ cosθ (sin θ)2 +(cos θ)2 =1 2sin 2θ+cos θ=1 ここで、三角関数の2 乗や3 乗は、(sin θ)2 =sin2 θTextbook solution for Algebra 2 1st Edition McGrawHill/Glencoe Chapter 141 Problem 41PPS We have stepbystep solutions for your textbooks written by Bartleby experts! 単位円を描いて考えると理解できると思います。 あるいは sin(θ-90°)=-cosθ cos(θ-90°)=sinθ と考えれば分かりやすいかと・・・




三角不等式 三角比 三角関数 おいしい数学




この問題でなぜ 答えが0になるのですか Clear
動経が1の場合、単位円の円周上の点pを、(x、y)のように表すなら、(cosθ、sinθ)となる。 また、sinもcosも、180(2π)を境目として、数値がループする。 180から360までの範囲は、 sin(180 θ) = sinθ cos(180 θ) = cosθ となる。



3




正割余割 三角関數 Retdy




90 8 180 8の三角比 Youtube




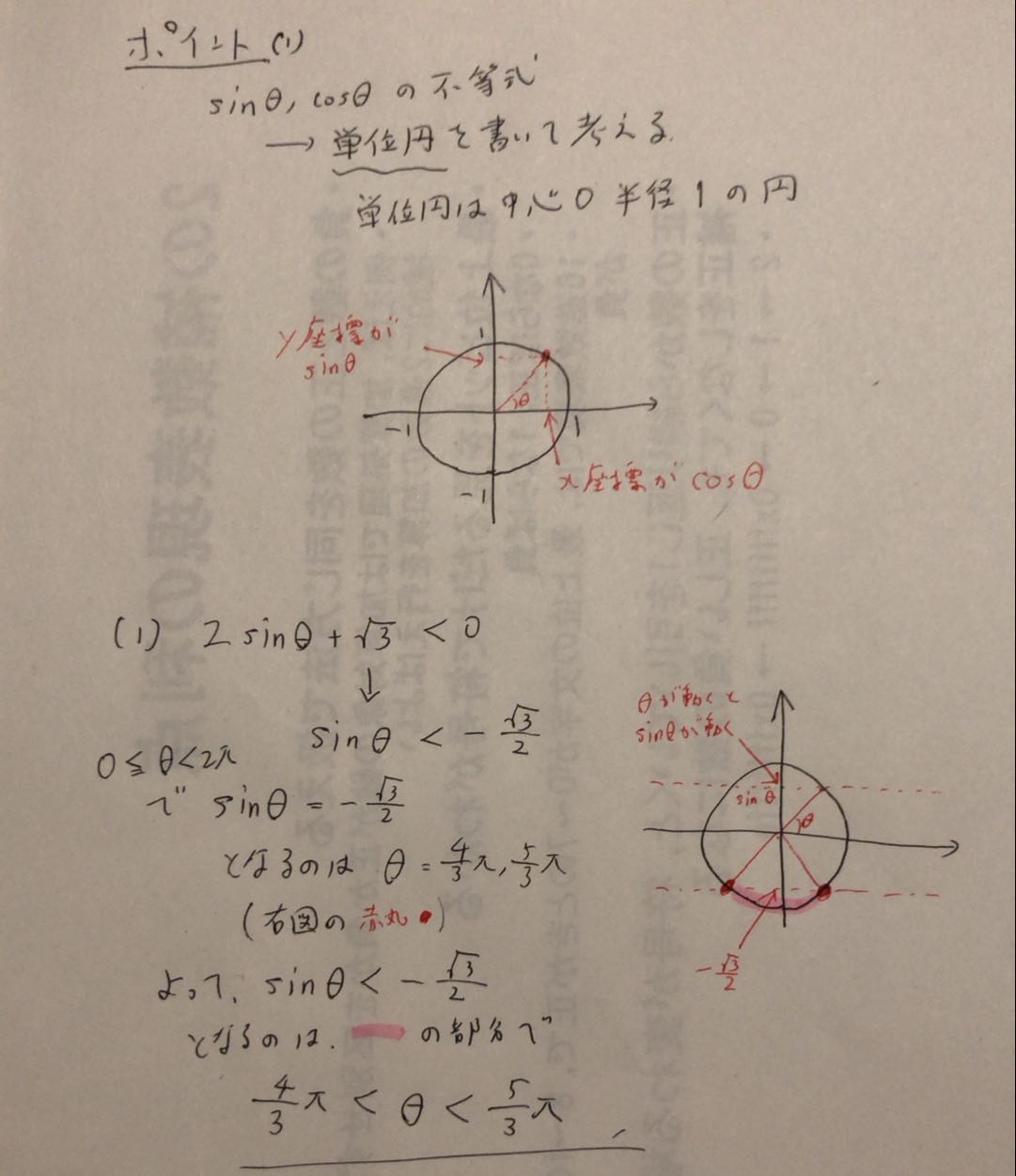
三角関数を含む不等式の解き方と単位円を使うコツ



48s96ub7b0z5f Net Sankakuhouteishiki Circle Graph



Http Www Eng Kagawa U Ac Jp Miyagawa Misc Math Basic Formula Miyagawa Pdf
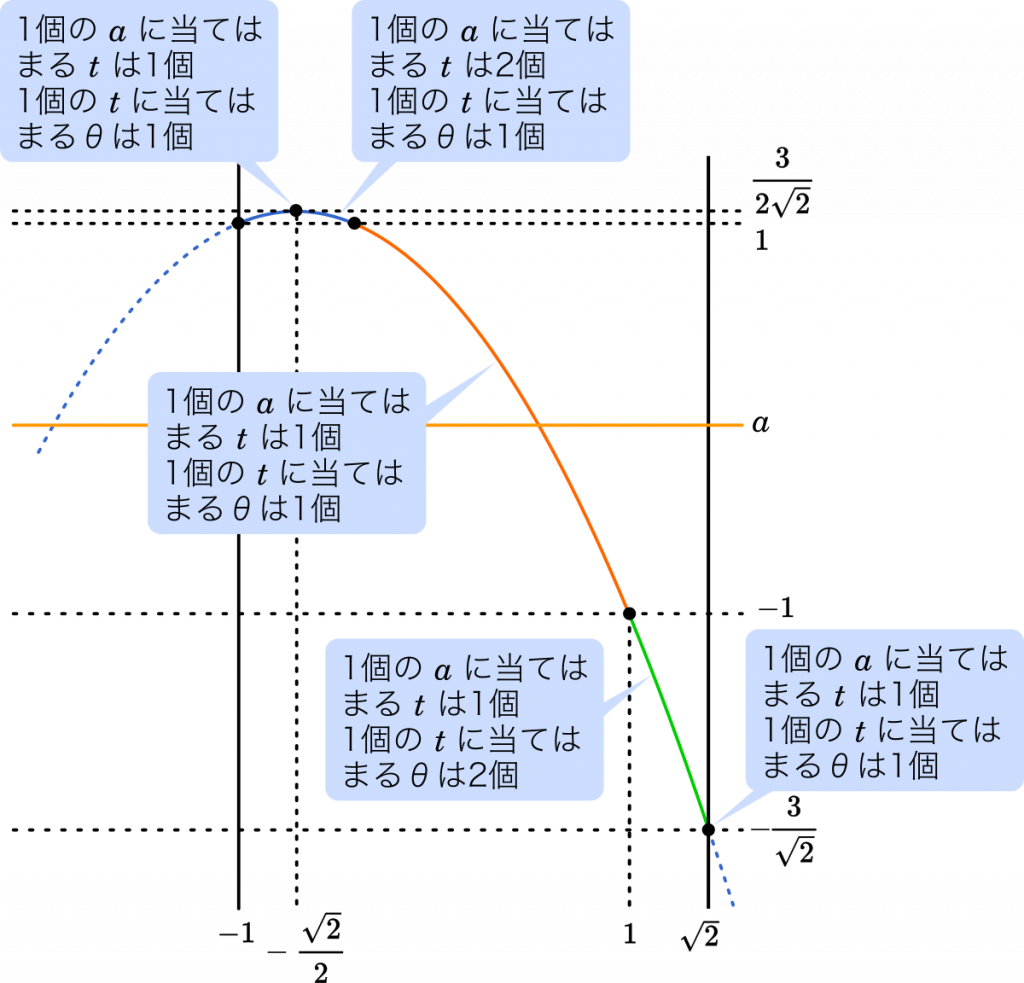



北海道大文系第2問 数iib三角関数 一つのsinに値に当てはまる8が1個のときと2個のときを判別する Mm参考書
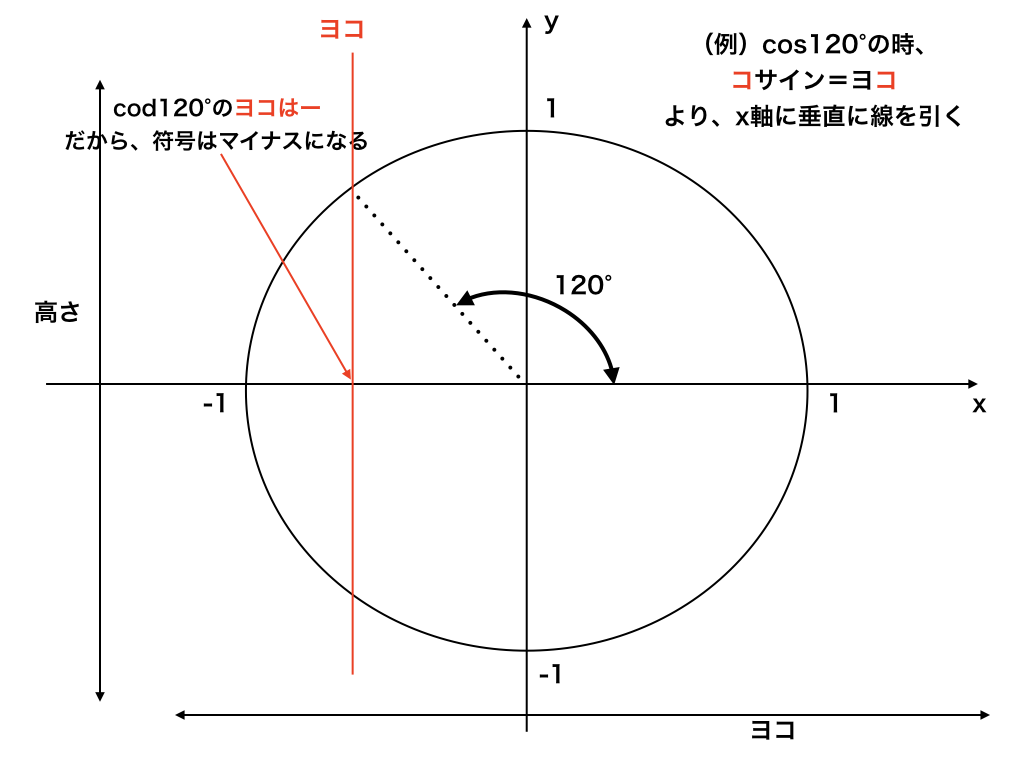



Sin 8 P 2 や90 8など還元公式の覚え方の解説 余角 補角の攻略




単位円を使いこなそう3 三角方程式応用編 Sin 8 P 4 1 Cos 8 P 3 1 2 Youtube
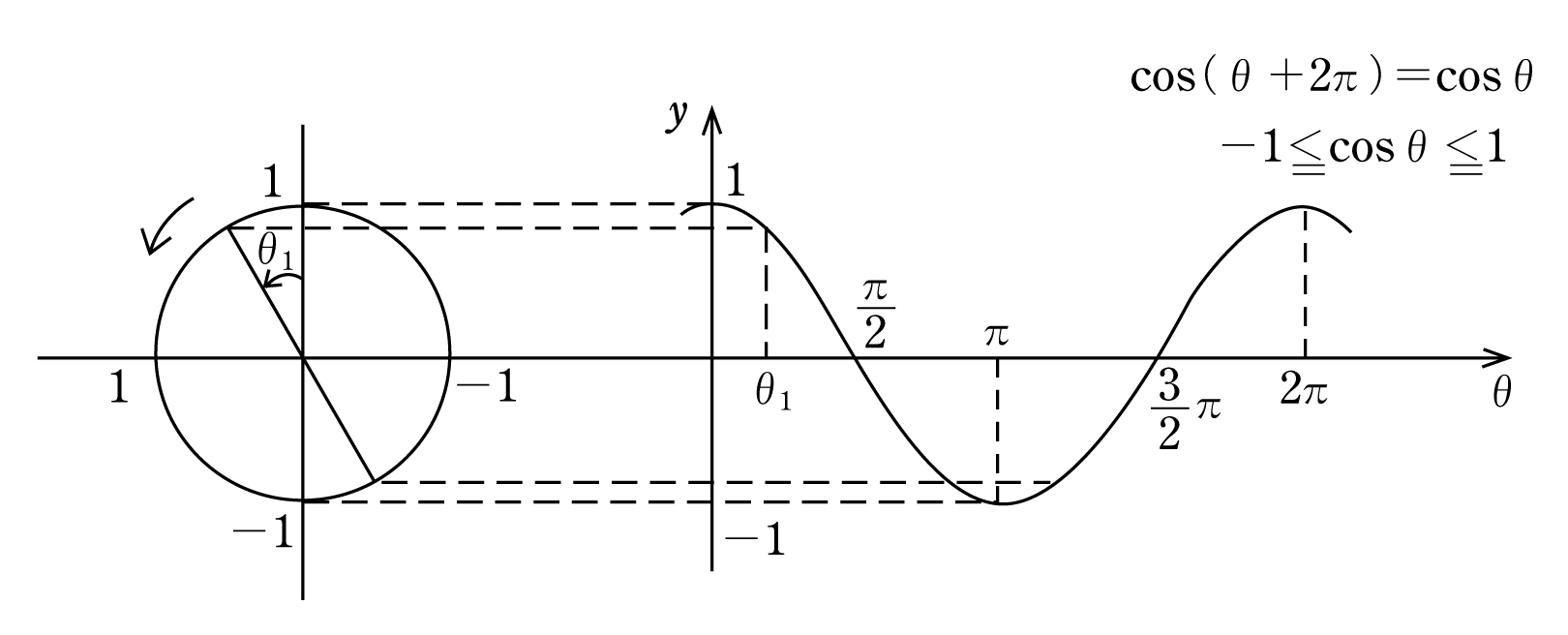



交流瞬時値の三角関数表示式 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会
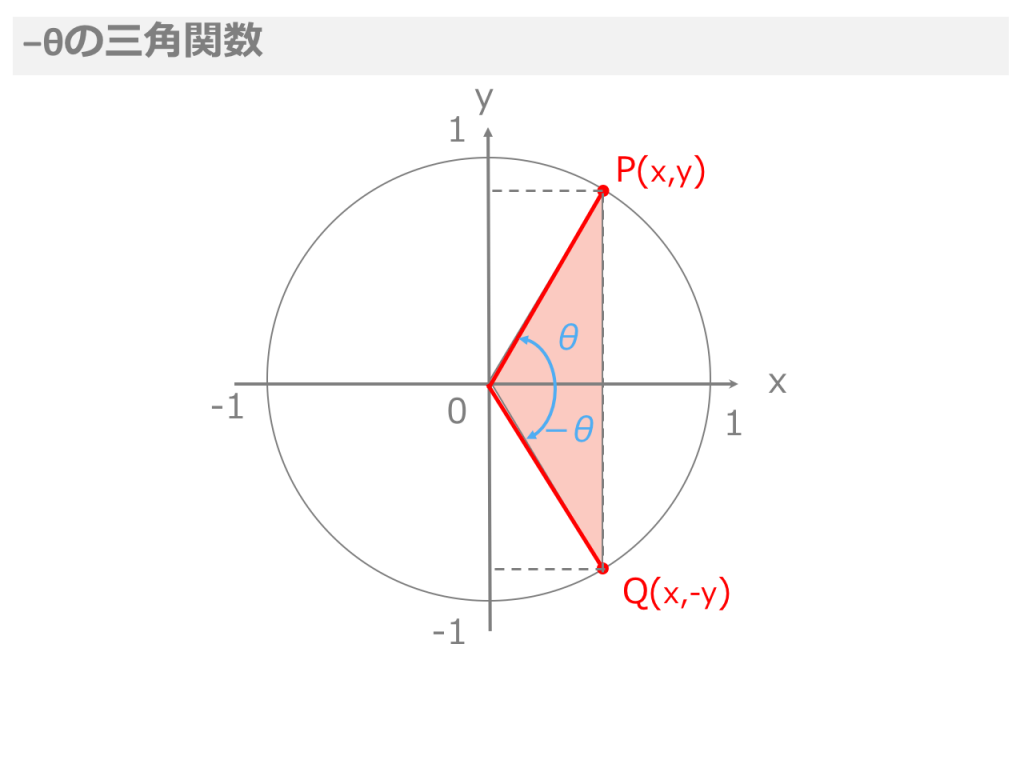



3分で分かる 三角関数の基礎知識 合格サプリ



Http Wasmath La Coocan Jp Sincostan Pdf




三角関数5 三角関数のグラフは縦や横から見るべし




F Sin2cos 0 Descubre Como Resolverlo En Qanda
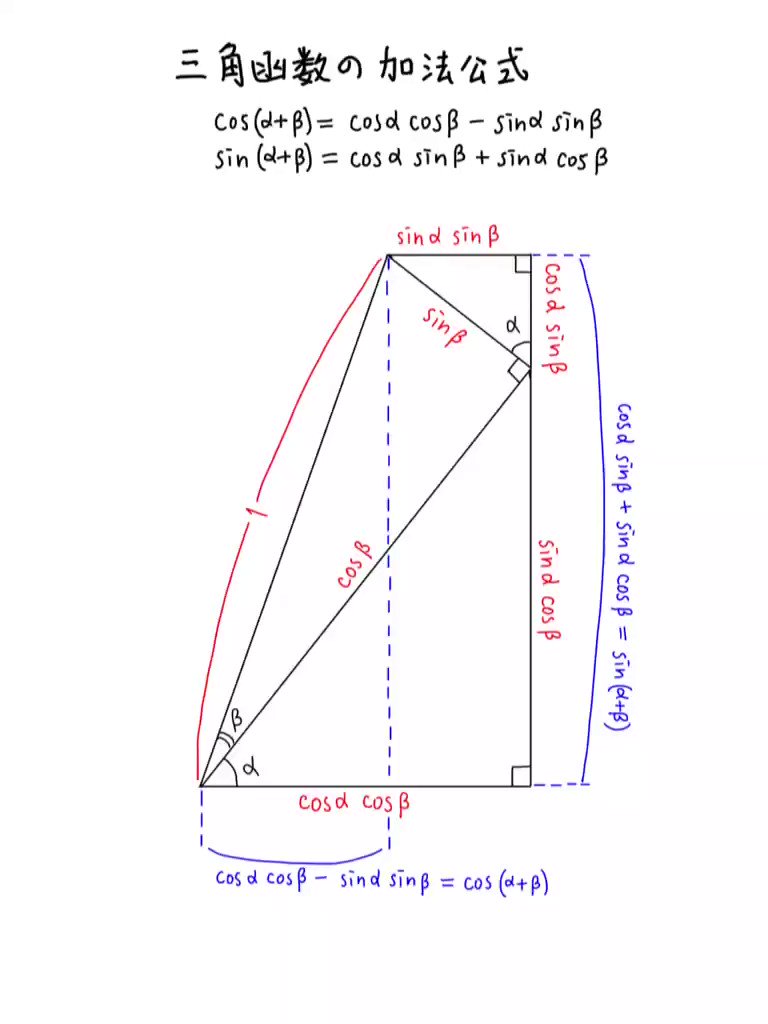



三角函数の加法公式



合格る一題 うかる一題 第1問 解答 解説 河合塾マナビス




J W R V Twitter 高校数学 数学ii 数学2 三角関数 Sin 8 P 2 とか Cos 8 P とかを簡単にする問題への統一的アプローチ 教科書の公式を全部覚えようとする人がたまにいるようである一方 学校



三角形の辺の比による三角関数の定義



Limg على تويتر Mathlava 更に訂正 誤 S U W H 2 正 S U 厳密には S U W H Cos8 Sin8 で 8 P 4 のときに U W H 2 となって 8 0 Or P 2 のときに U W H となる ここは W とh から面積を出さずに 単に S U と考えた




三角関数の加法定理と余弦定理の証明 Nibosiiwasi S Blog
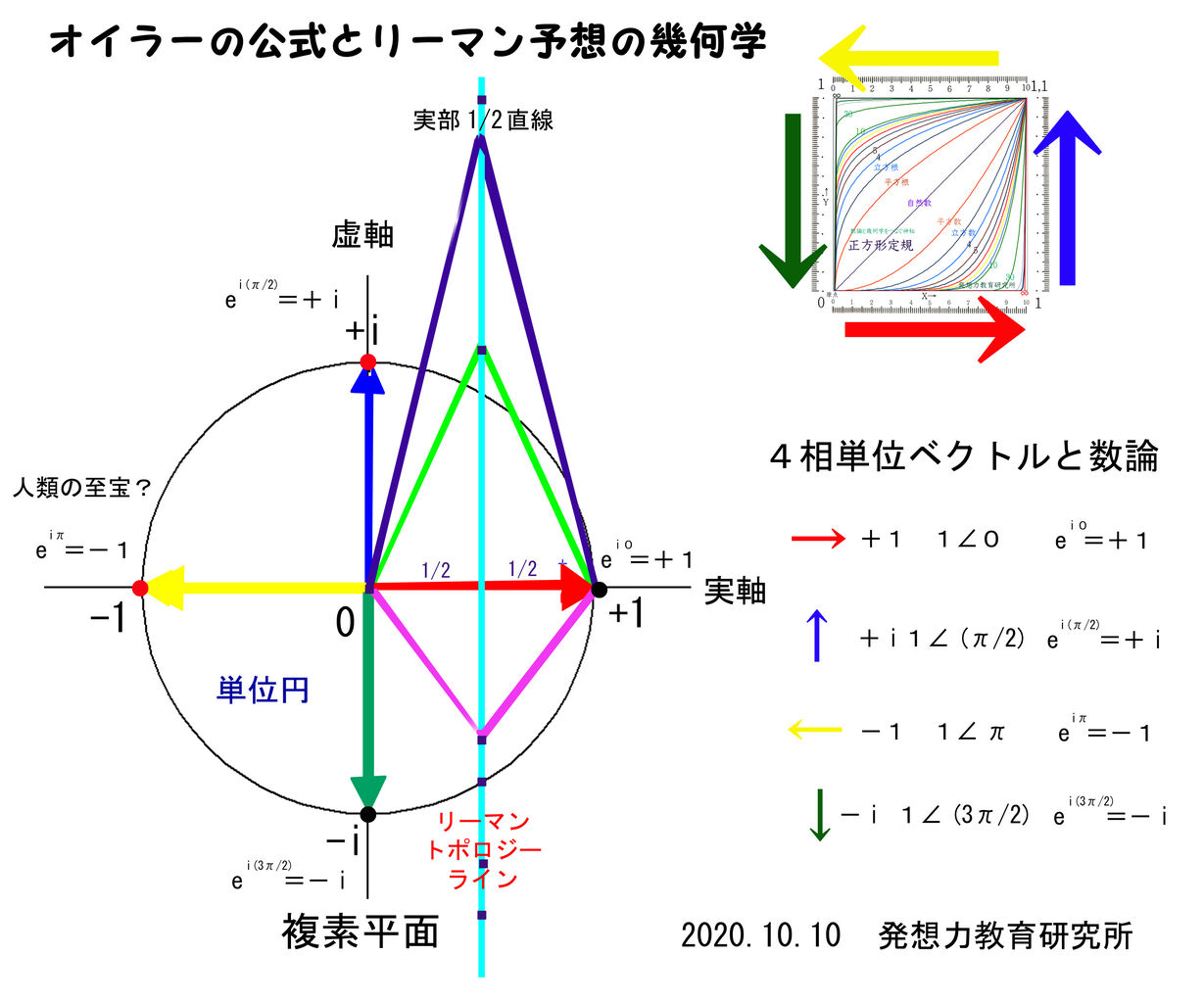



オイラーの公式 E I8 Cos8 I Sin 8 で絶対値 Cos8 2 Sin8 2 1と言えるのは8 0 90 180 270 の時だけである 発想力教育研究所 素数誕生のメカニズム
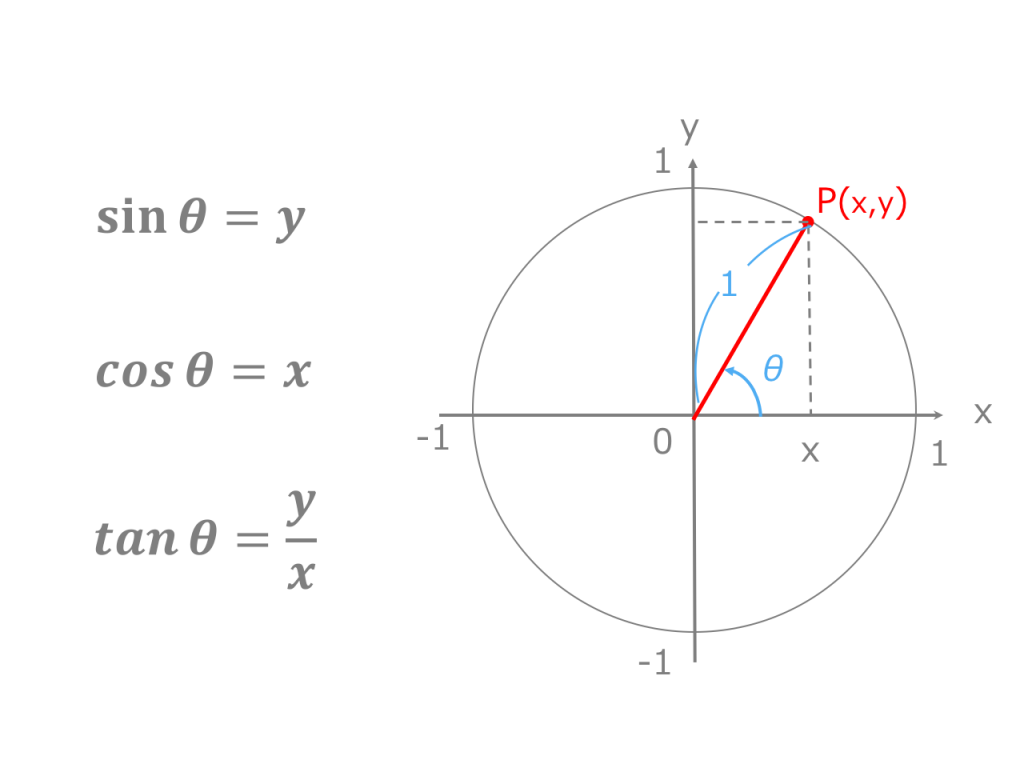



3分で分かる 三角関数の基礎知識 合格サプリ




0dfracpi2 Sin4cos 0 Lihat Cara Penyelesaian Di Qanda
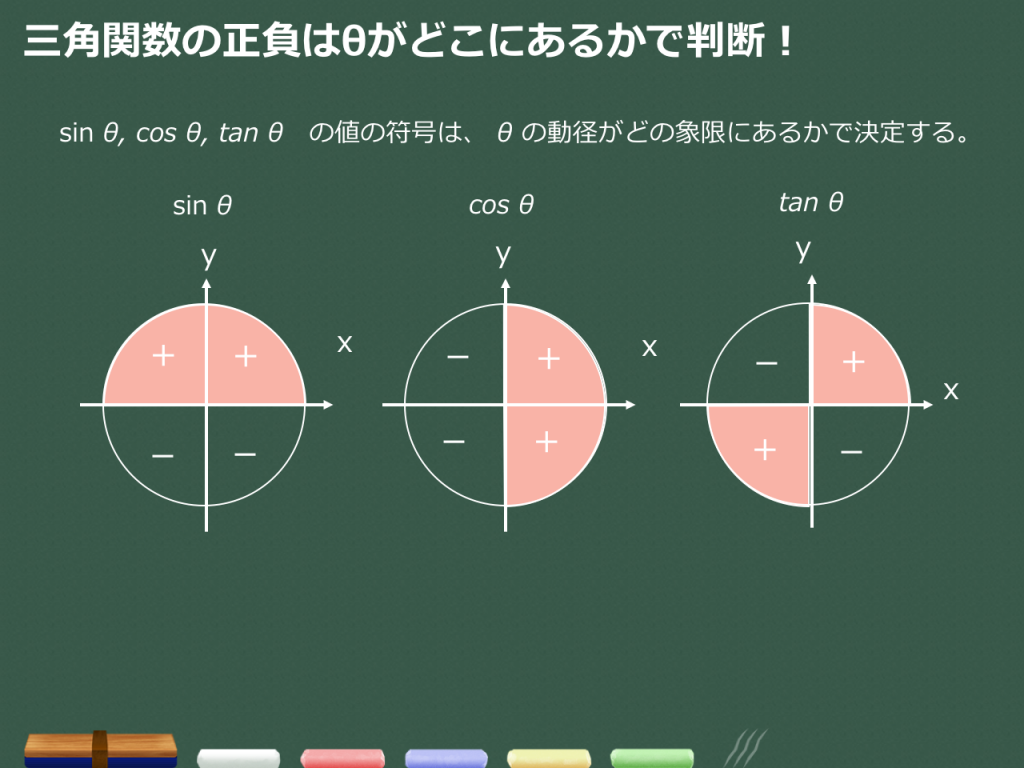



3分で分かる 三角関数の基礎知識 合格サプリ



3



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典




解説読んでも分かりません 教えてください Clear
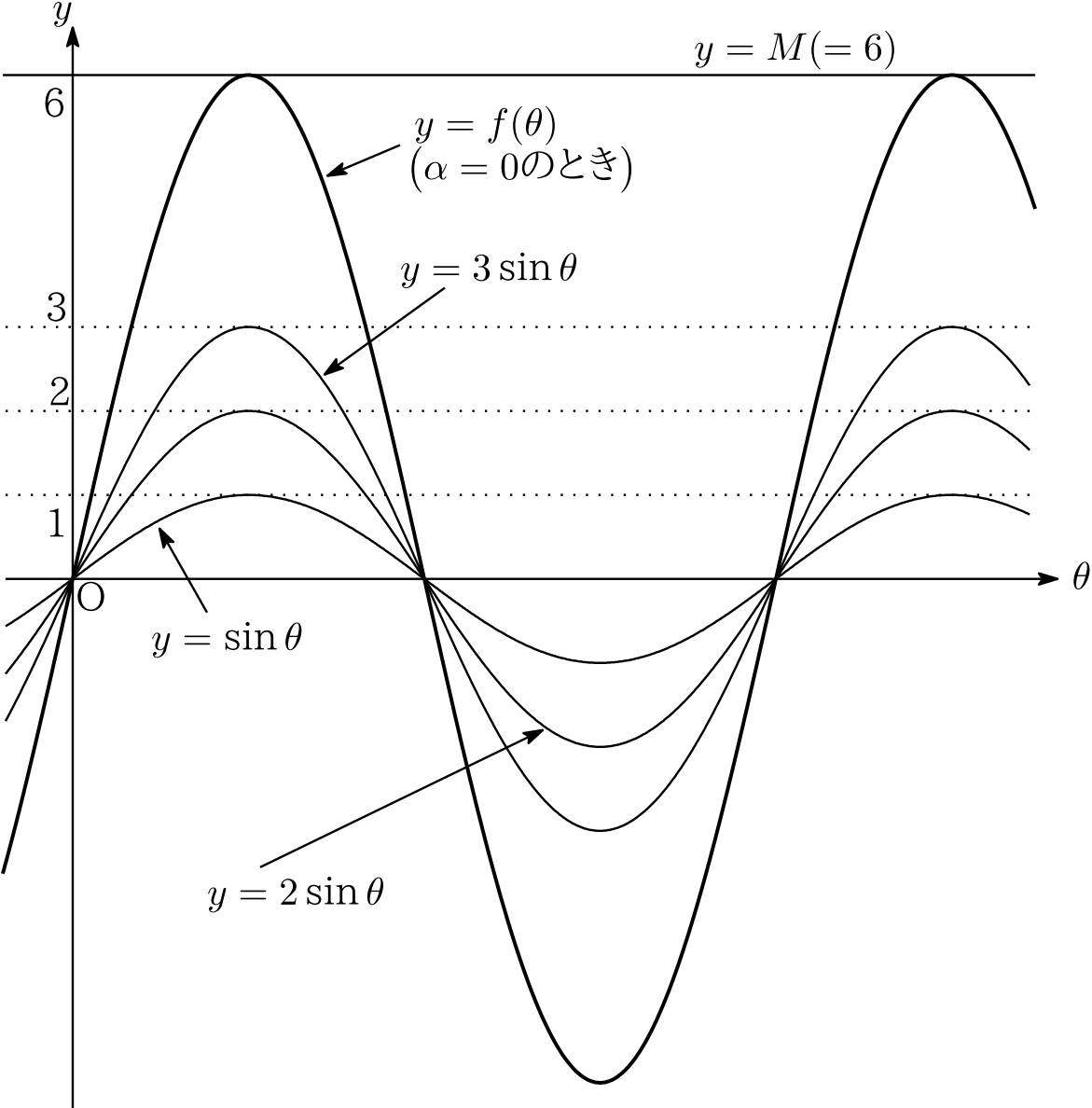



合格る一題 うかる一題 第1問 解答 解説 河合塾マナビス




P 2 8 P 2の範囲って単位円で書くとどんな感じになりますか Clear




三角方程式 おいしい数学
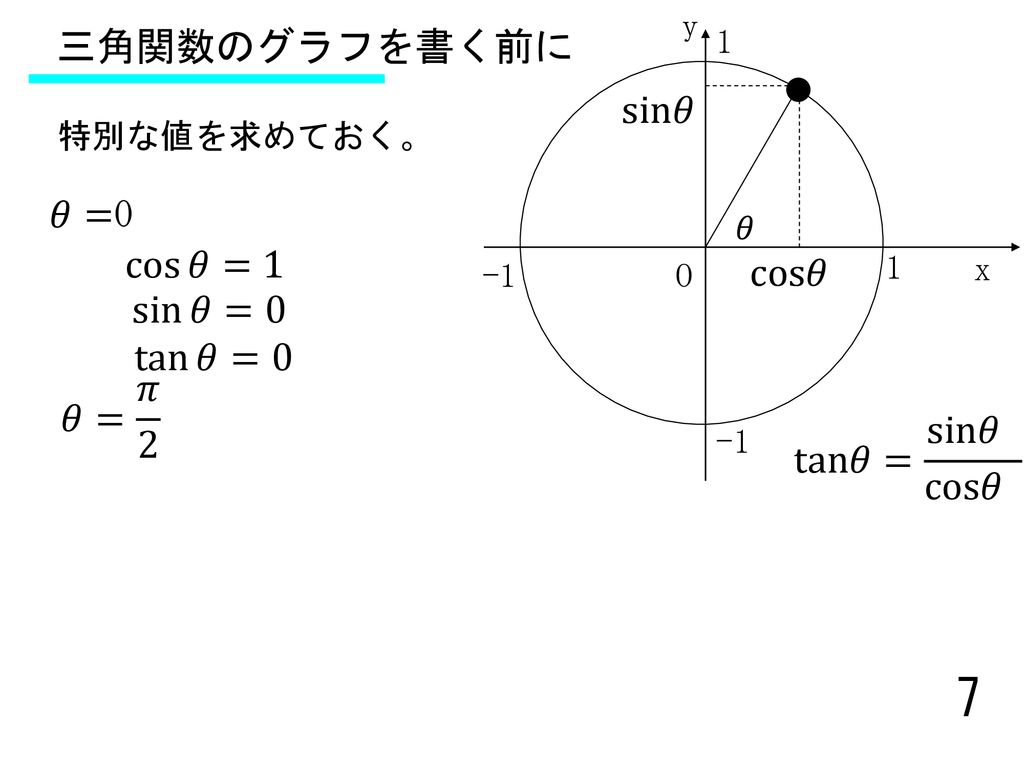



振動と波動の準備 三角関数の復習 定義と微分 三角関数は 物理でよく使います Ppt Download




16 合成公式はsinだけじゃないんです 医学生gの数学ノート



交流瞬時値の三角関数表示式 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会



三角形の辺の比による三角関数の定義



第7話 補遺 Hirosi Ooguri




交流瞬時値の三角関数表示式 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会




Unit Circle Wikipedia




曲面積の求め方 Notes Jp




三角関数の加法定理とその証明 おいしい数学



数学の基礎概念
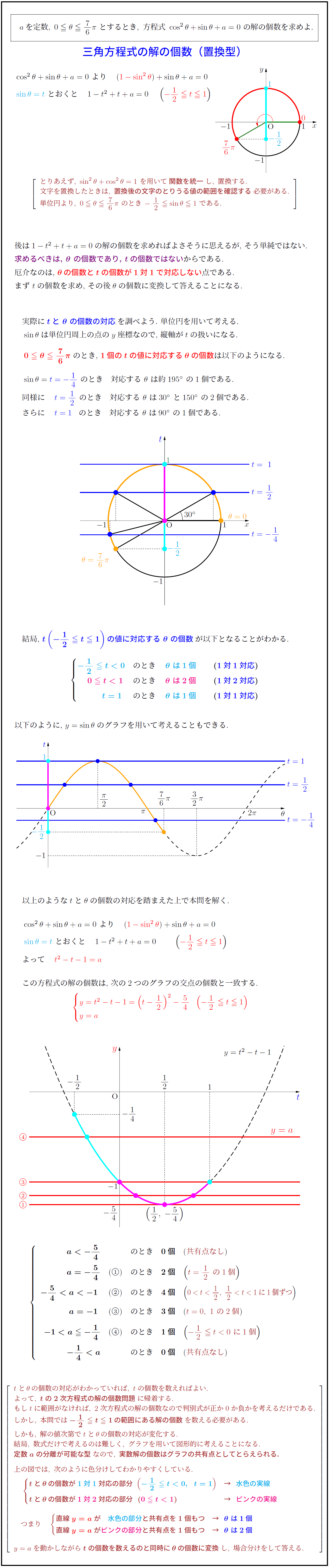



高校数学 三角方程式の解の個数 置換型 受験の月



Sin 8 P 2 や90 8など還元公式の覚え方の解説 余角 補角の攻略



48s96ub7b0z5f Net Kahouteiri 15 75



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



3




第1章 三角関数の極限と近似




Sin Cos Tan 公式覚え方 三角比 三角関數の基礎sin Cos Tanが簡単に分かる解 Gkgnae




三角関数の加法定理と余弦定理の証明 Nibosiiwasi S Blog




解説読んでも分かりません 教えてください Clear




解説読んでも分かりません 教えてください Clear




数学 三角関数 三角関数の相互関係 オンライン無料塾 ターンナップ
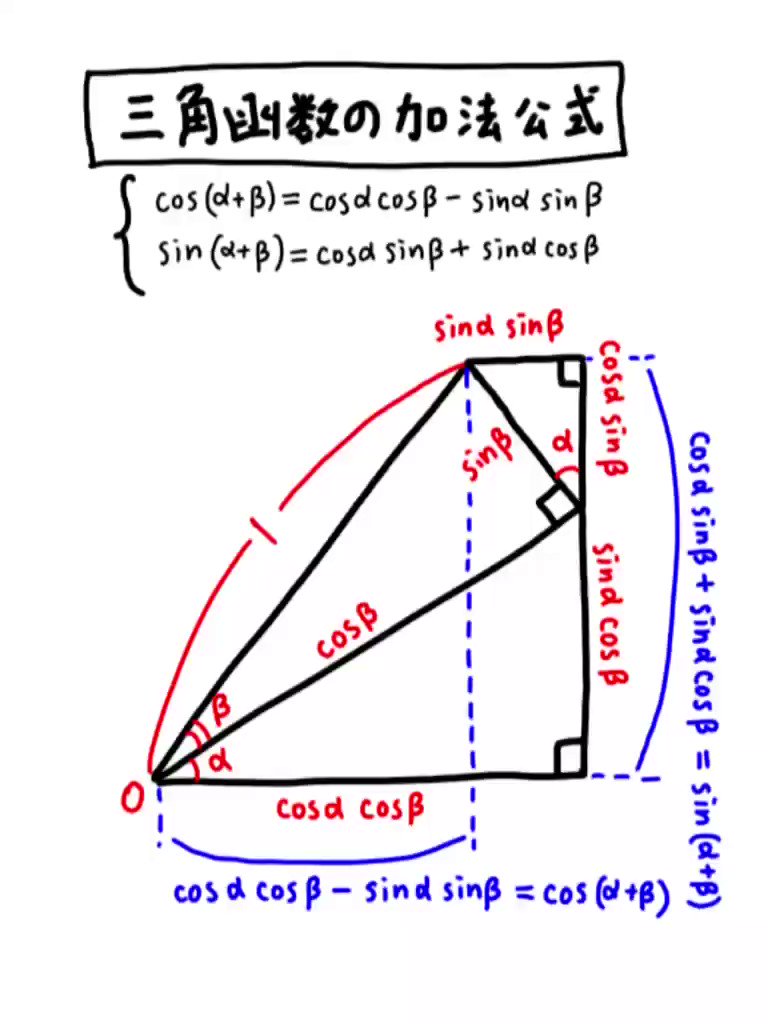



三角函数の加法公式




三角関数の加法定理と余弦定理の証明 Nibosiiwasi S Blog



48s96ub7b0z5f Net Sankakukansuu Baikaihensuu




J W R V Twitter 高校数学 数学ii 数学2 三角関数 Sin 8 P 2 とか Cos 8 P とかを簡単にする問題への統一的アプローチ 教科書の公式を全部覚えようとする人がたまにいるようである一方 学校でこの処理法を触れないことが多いようなので T Co Mailhw9stf



数学 三角関数について整理する Qiita




三角関数を含む不等式の解き方と単位円を使うコツ



合格る一題 うかる一題 第1問 解答 解説 河合塾マナビス




三角関数 1 0 X 2pのとき 方程式 3 Sinx Cosx Okwave




第7話 補遺 Hirosi Ooguri
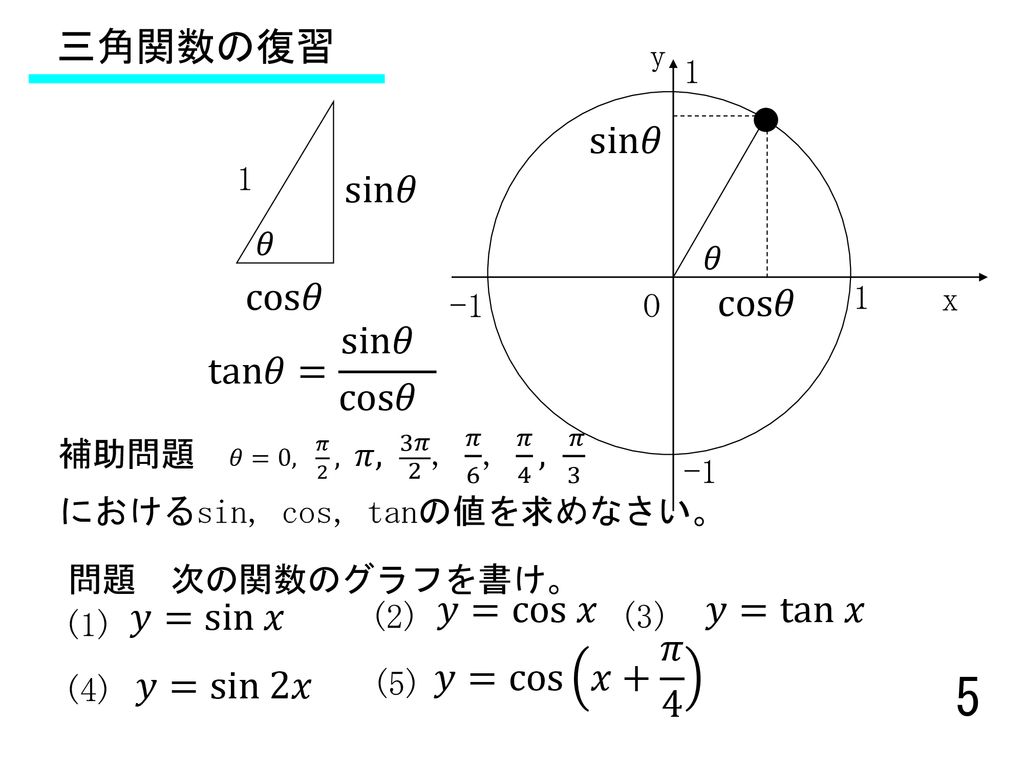



振動と波動の準備 三角関数の復習 定義と微分 三角関数は 物理でよく使います Ppt Download



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典




Xsqrt Barxsin Sqrtdfracp Descubre Como Resolverlo En Qanda




2pnとは いるんですか 解かなと思った答えに必ずついてきます Okwave



3




F Sin2cos 0 Descubre Como Resolverlo En Qanda




解説読んでも分かりません 教えてください Clear
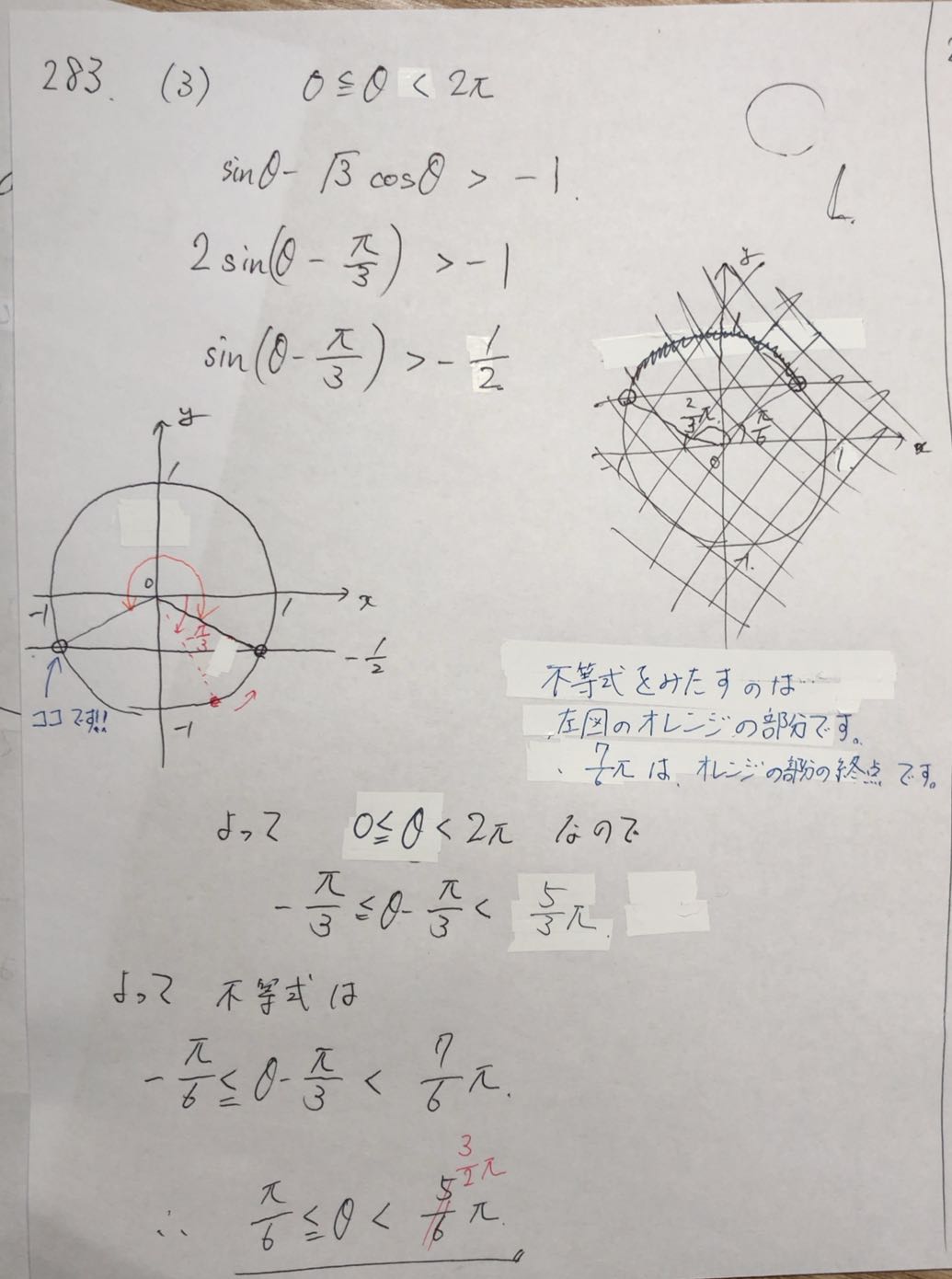



Pleft Abright 281 1 Y Descubre Como Resolverlo En Qanda




三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ



48s96ub7b0z5f Net Sankakukansuu Seishitsu



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典




三角方程式 おいしい数学



工科系数学i及び演習 17年度前期 第17 18 19回



三角形の辺の比による三角関数の定義




三角関数 合成はやり方と目的さえわかれば克服できます 大学受験数学の解き方



Sin8 1 3 P 2 8 P 2 であるときのsin 8 Cos8 Yahoo 知恵袋




8 2np 8 8 P 8 P 2 P 8 P 2 8の三角関数 数学ii 三角関数 7 Youtube



交流瞬時値の三角関数表示式 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会



48s96ub7b0z5f Net Sankakukansuu Koushiki
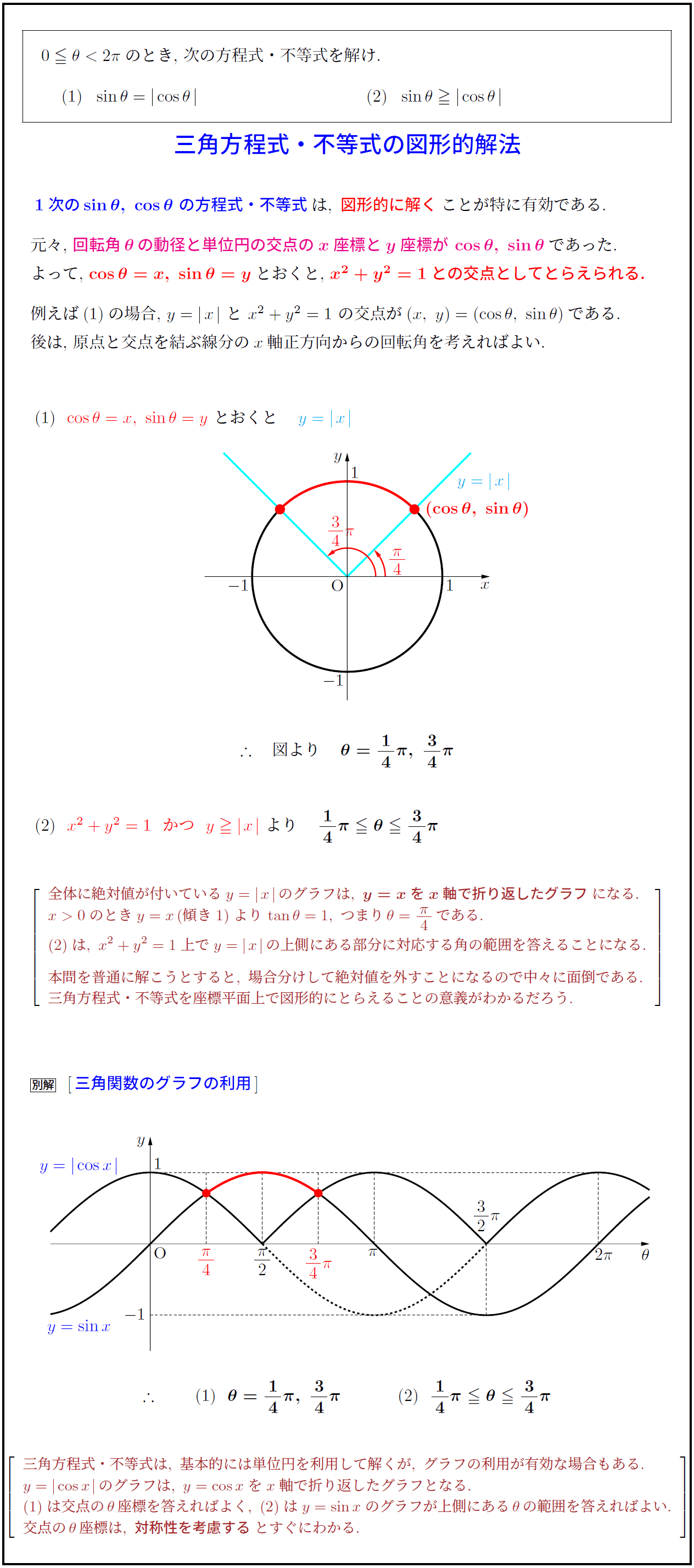



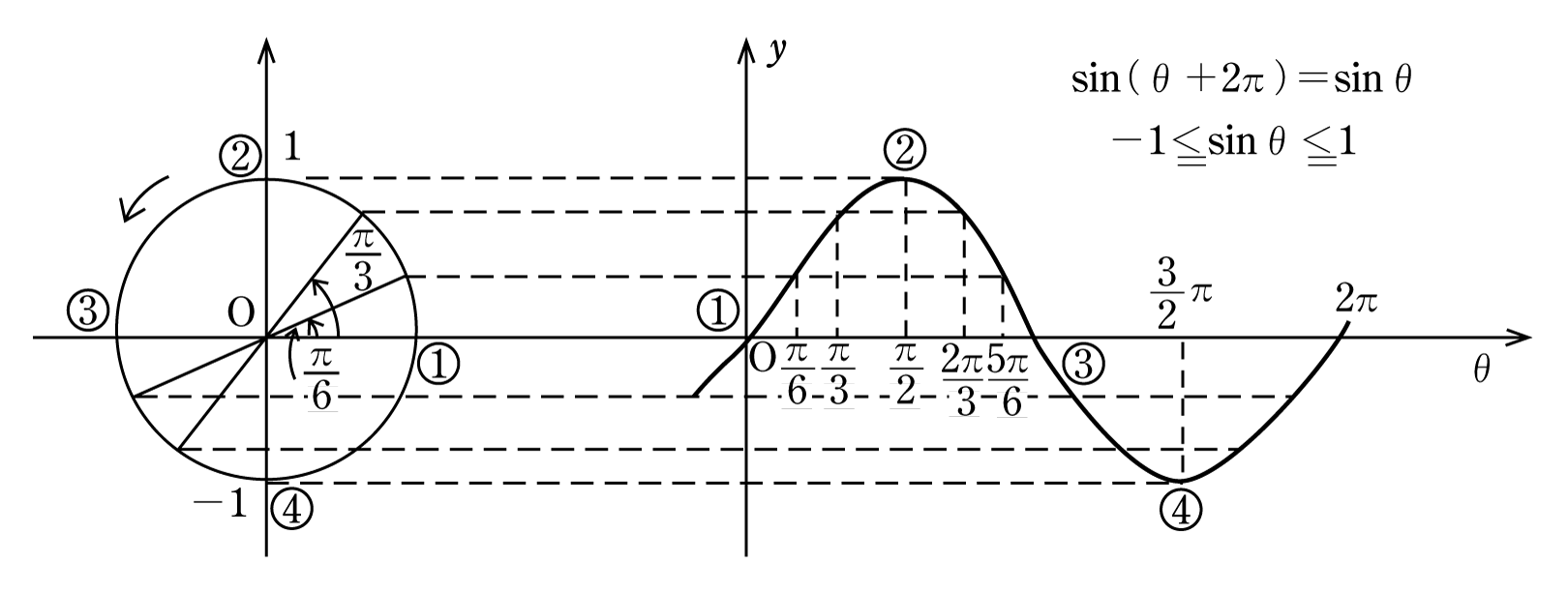
高校数学 三角方程式 不等式の図形的解法 座標変換 グラフの利用 受験の月
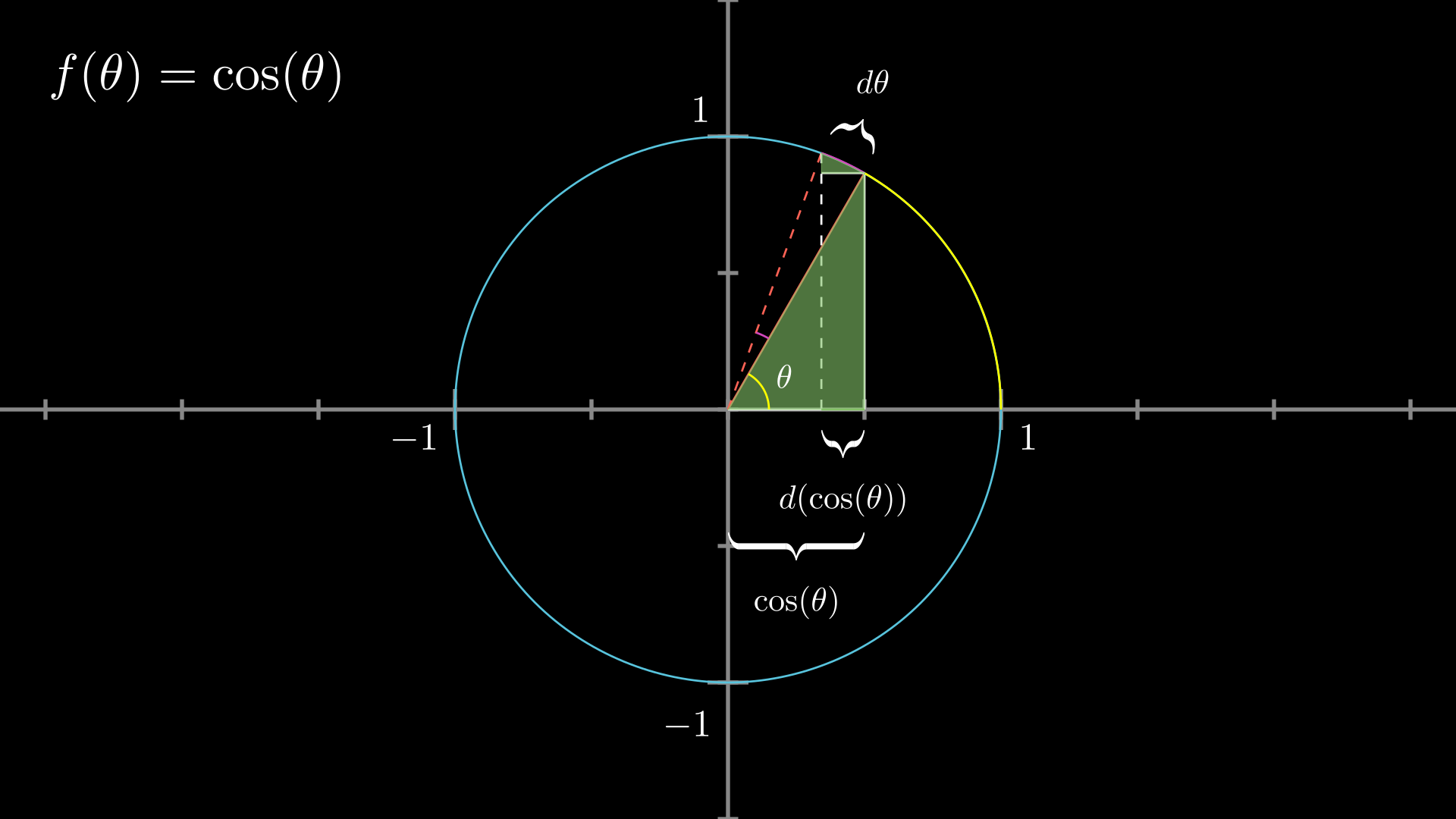



三角関数の微分を誰でも驚くほどよく分かるように解説 Headboost




三角関数についての質問です 8に関する方程式sin8 Kcos8 2 Okwave



複素数平面の質問です 例題6と37番の 2 の解説をして欲 Yahoo 知恵袋



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典
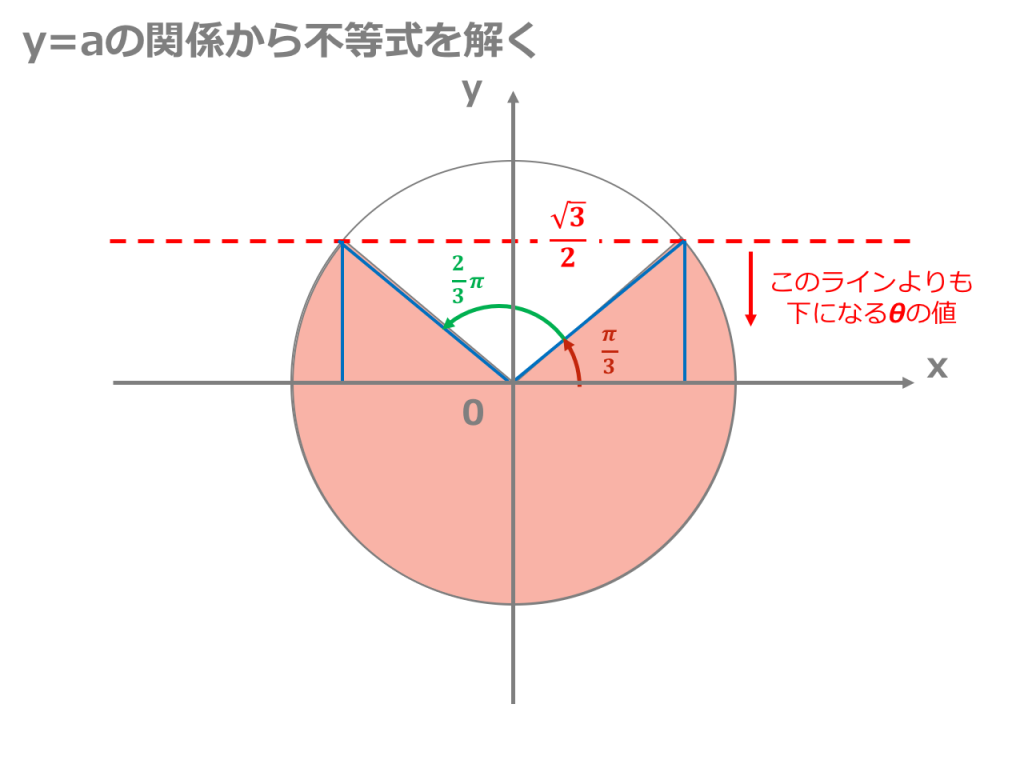



3分でわかる 三角関数の不等式の解き方 合格サプリ



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典




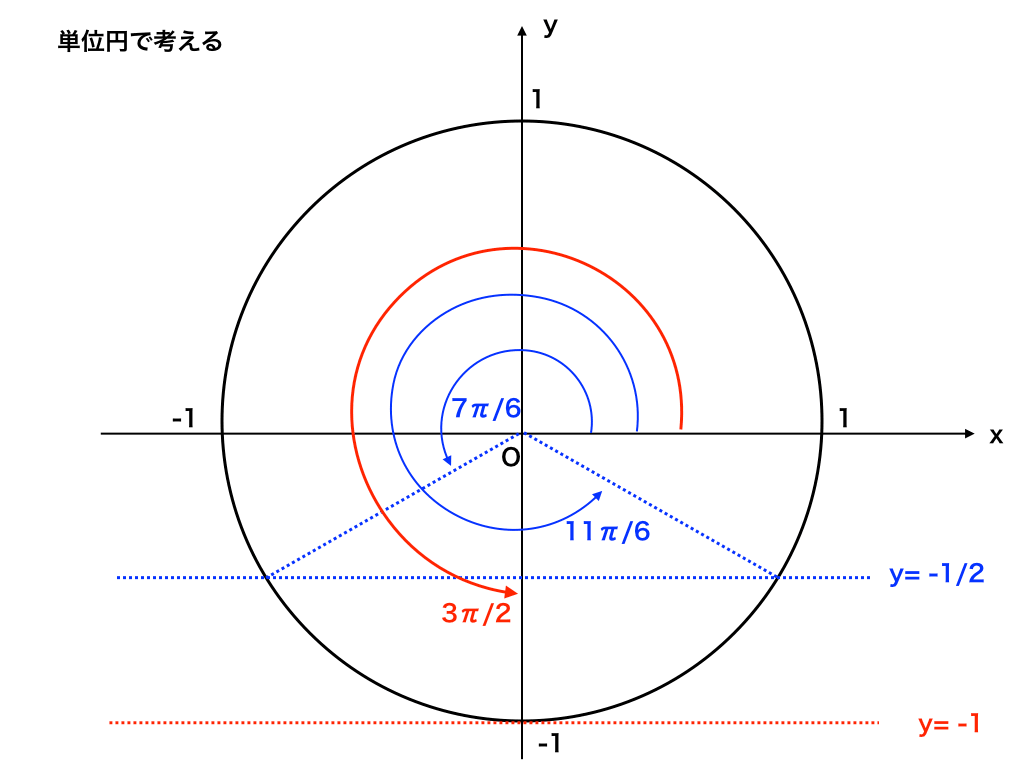
三角関数の性質を単位円で理解する 8 2np 8 P 8 P 2 8 大学受験の王道



0 件のコメント:
コメントを投稿